2026春 2025春 2024春 2023春 2022春 2021春 2020春 2019春 课程号:PHYS7604P01
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:一般
| 选课类别:基础 | 教学类型:理论课 |
| 课程类别:研究生课程 | 开课单位:物理学系 |
| 课程层次:博士 | 学分:4.0 |
教学水平与内容
段昌奎老师的《群论及其应用》课程内容多样且丰富,主要参考教材为Dresselhaus的《Group Theory: Application to the Physics of Condensed Matter》。课程涵盖群的基础概念、群表示论、特征标、基函数、跃迁选择定则、分子轨道、空间群及其表示,以及更多高级内容如双群与时间反演对称性。教学资料凝练,板书脉络强,但部分学生认为讲课内容跳跃,需课下自行学习和参考书目补充。此外,课程特别适合学过特征标的学生。
作业与助教
课程没有指定作业,助教由高年级博士生自愿担任。建议有兴趣的同学课下自学,并练习课本的习题。由于缺乏系统性的练习安排,课程要求学生更多的自主学习。
考试与难度
考试题目的质量和难度受多位同学讨论。部分学生认为考试题目较难且不按套路出题,需深入学习才能应对。今年考试有题目偏难且与物理应用相关。最近的调分政策较为慷慨,表现欠佳的同学也获益良多,调整后的成绩普遍较高。
给分
段老师在评分上较为宽松,不少同学表示其总评分大幅高于卷面分。今年无学生挂科,调分幅度达15分,具体成绩分布较为理想。
总评
综合来看,虽然部分学生对上课方式不满,认为需要更多自主学习,但课程在凝聚态物理中的应用价值及内容覆盖度受到好评。课程实用性强,适合对相关群论概念有初步了解并愿意进行自主学习的学生。选择该课程需有充分的心理准备,并把握好学习节奏和参考书籍。
- 课程难度:困难
- 作业多少:很少
- 给分好坏:超好
- 收获大小:很多
- 难度:困难
- 作业:很少
- 给分:超好
- 收获:很多
不能苟同楼上那位同学的观点!以下逐点分析反驳:
1.“老师上课内容明显没有充分备课,经常会卡壳、举不恰当(或者有失一般性)的例子”。事实上,老师每节课前都会备课,这点我曾经和老师交流过。举的那些例子我个人认为十分便于理解抽象的定理,一些不太恰当的表达(比如讲解李群时)也是为了学生更好理解。
2.“PPT和讲义也不像是这个年代该有的,排版十分混乱,上课很难跟随”。只有空间群部分的讲义排版混乱,李群部分是从书上择出来的,老师怕学生看不下去英文书所以拣了最重要的定理拼成了图。至于能否跟随思路,我觉得这是个人问题。
3.“如果要学好这门课,不仅需要上课听老师讲,还会有很多老师上课讲不明白(他自己表述能力有问题或者他也不明白)的地方需要自己下课去看各种参考书”。这点部分认同,确实需要课下去看《Group Theory:Application to the Physics of Condensed Matter》(此书是前半学期的课本)上的例子。但说老师表述有问题我就纳闷了,如此抽象的李群李代数我都听明白了,这恐怕不是表述有没有问题,而是你有没有认真听课的问题了。
4.“试做2024往年卷,感觉老师出的题目除了和他做的光谱学相关的方面以外,质量很差;例如有写出P(4)置换群的所有非平庸子群这种毫无意义的题目,不知道老师本人是如何处理这种没有通解,只能自己硬凑的题目,我是不知道在数学和物理应用中,写出一个24阶群的所有非平庸子群有什么用”。P(4)同构于Td点群,而点群的母子群关系是相变过程中晶体结构对称性改变的依据。这种关系不但本身有用,而且是空间群母子群关系的基础。比如,问一个立方体(Oh对称性)沿体对角线(即(111)方向)拉伸或压缩后得到分子具有何种对称性?这正是今年考试第一大题的第一问,去年的题更简单但也更繁琐,却并非不重要。
5.“隔壁的物理学中的群论讲的十分有逻辑清晰”。这是我认为最颠倒是非的一条。首先,朱界杰老师严重详略不当。前面讲群论基础、线性表示理论和转动群花了太多时间,导致非常重要的点群和李群开起了快车,没接触过的听的一头雾水。而且他考试明明不考证明题,却花了许多功夫证明那些定理。这点段老师做的就很好,关于特征标、李代数的各种定理证明我们做物理的关注它干什么?不是重点的东西段老师就让我们感兴趣自己去看书,不想看并不耽误考试,想看的一学期下来也能有额外收获。其次,朱老师讲的过于抽象,不够切实。为了引入李群,要先讲拓扑空间、微分流形等等一堆让人望而却步的东西,末了给出李群的定义:李群是一个复合结构(X·,T,A),也是n维光滑流形。听君一席话,如听一席话!而段的讲义中给出的李群定义是:

哪种方式更便于学生理解,我想不言自明。
接着我来说说真正劝退的点,就是这门课要学的东西非常多,选课前一定要做好心理准备。除了基础的群论和群表示论、点群空间群、李群李代数、双值群、置换群,最后半个月还讲了时间反演对称性和磁点群,不过考试不考。推荐学过特征标这些内容的同学来学,而且即使之前学过一部分课下也要花时间消化吸收。不过既然不布置作业,那就是希望你自学的。都是博士生了,愿不愿意自学全看个人,我认为总比朱界杰作业布置了一堆证明题结果考试不考要强。但要是平时一点不听,妄图考前临时抱佛脚,那还是找老师签退课申请表吧。
尽管开课时威胁会给人挂科,但实际上段老师是非常心慈手软的。今年调分就非常给力,我总评分比期末卷面分足足高了15分,如果卷面成绩差的会高更多。今年也没有人挂科,具体成绩分布如图所示
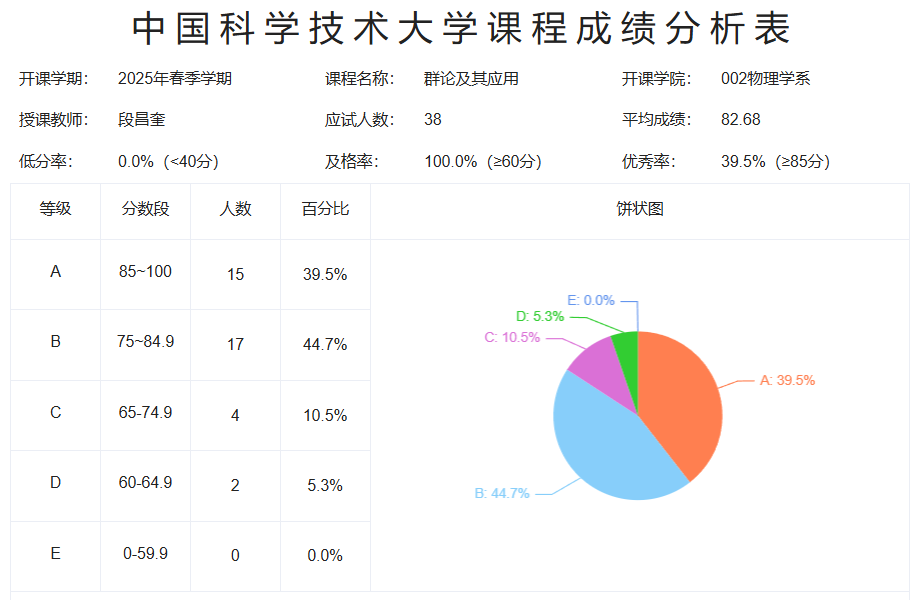
最后附上最近三年的考试题目。2023年的第一题确实偏了点,D4d不是晶体点群,特征标表不容易查到。

以下是原评论:
笑死,开课前我天天刷教务系统,总是人满选不了,加课申请表都打印好了准备让老师签字。结果今天上课老师说去年有四五个人挂科了,立马有人退课了🤣
- 课程难度:中等
- 作业多少:很少
- 给分好坏:一般
- 收获大小:很多
- 难度:中等
- 作业:很少
- 给分:一般
- 收获:很多
之前的评论不知道怎么回事找不到了,我再写一遍吧。
首先单纯论内容而言我觉得这个课对于凝聚态的学生是非常有用的。第一次觉得将群论这个数学知识实实在在地在固体物理上进行了应用。用的课本主要为Dresselhaus写的Application to the Physics of Condensed Matter,但没有讲完,实际上我觉得后面没有讲完的用处会更大,但是课时受限。但我觉得这本书写得是不错的,没有什么晦涩的句子,读起来是挺滑溜的,以后可能会抽时间自己再学一下后面的电子声子色散部分。
具体授课内容为:第一章群的基础概念,第二章第三章群表示论与特征标,第四章基函数。这部分内容也是朱的群论完美覆盖的。第五章简单介绍了一下转动群然后就是原子在晶体场作用下能级如何劈裂。第六章讲了跃迁选择定则。第七章讲了分子轨道,第八章是分子振动模。第九章第十章空间群和其表示,但是这部分书上的内容实在是过于羸弱,老师结合其他教材补充了不少知识,但我备考时只是匆匆看了一遍书,所以印象实在不深刻。这学期又多上了十四章的双群与SOC,16章的时间反演。
再有就是教学方面。首先说一下优点。老师在讲课的时候会将教学内容整理成笔记,比较凝练,会给复习(预习)提供很大帮助,而且会补充很多东西,板书的脉络性也是比较强的。缺点是我觉得段老师思维对于学生而言有些跳跃了,提前了解内容的话会觉得收获不少,如果是白板听课的话可能就要注意力稍微集中一点...这门课没有助教,助教是老师组里的高年级博士生自愿当的,所以也没有作业,想做作业的话可以自己把课后习题做一遍。
最后再说一下考试,考完我就觉得自己寄了,今年考了三道题,跟往年比我觉得更难一些,做卷子感觉有种不能套路出牌的感觉,及其麻爪,不知道从何做起,可能也跟个人水平有关系确实学得不太深入。最后卷面分3.1,调到了3.7,谢谢老师。